今天来复习一波贪心算法。贪,就完了~~~
一、贪婪算法
贪婪算法(Greedy Algorithm),又称贪心算法,其主要思想是:在每一步决策中,总是选取当前状态下最好的或最优的选择,从而希望得到的最终结果是最好或最优的。即希望通过实现局部最优来达到全局最优的目的。 ——贪心算法-WIKI
贪心算法具有无后向性,即每一阶段的决策一旦确定,这个决策结果都不会受到后面的决策的影响,且不能回退回到之前的某一状态。这与动态规划有所区别,动态规划会保存之前的运算结果,包括选择或未选择的运算结果,并能够根据以前的结果来对当前的结果进行选择。因此,对于大部分问题,贪心算法并不是一定是能够取得最好或最优结果的算法,只能取得较为接近最好或最优结果,因而它的应用范围有限。
下面来上点典型应用,加深认识和理解👇👇
二、贪婪算法的典型应用
先来上点开胃菜,👇👇
1.找零钱问题
有几种固定面额的纸币,比如100块,50块,20块,10块,5块,1块。当需要找数值为n钱额的零钱,问如何找才能使得所找的纸币数量最少?
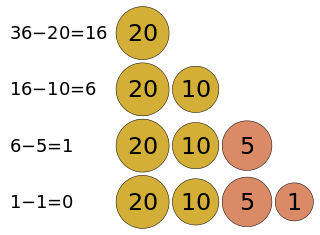
这很明显的贪心问题。当然每次找最大,以一抵十、以一抵百,这样纸币数才是最少。具体实现思路可以转换为:每次找在n范围内最大面额的纸币,然后n减去所找的纸币,再重新找下一张纸币,直到最后n=0。换一个角度,每次都贪面额最大的纸币,每次都贪面额最大的纸币,每次都贪面额最大的纸币。贪着贪着就找完了,得到的纸币数刚好是最少的,也得到了问题的最优解。
2.背包问题

背包问题是贪心算法和动态规划里最经典之一了。背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。——背包问题-WIKI
考虑物品数量为1的情况下,根据物品是否可分量可以分为一般的背包问题和0-1背包问题。
- 一般的背包问题中,可以将物品的一部分装入背包,但不能重复装入。
- 0-1背包问题中,限定每种物品只能选择0个或1个。即要么装完一整个要么不装,与部分装入相对应。
这里,我们分开讨论(空谈太乏,上个例题):
背包问题
给定N个物品和一个背包,背包的容量为W,假设背包容量为15,第i个物品对应的体积和价值分别为W[i]和v[i]。各种物品的价值和重量如下:
| 物品编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 重量W | 3 | 4 | 7 | 8 | 9 |
| 价值V | 4 | 5 | 10 | 11 | 13 |
求: 如何选择装入背包的物品,使得装入背包的物品的总价值为最大。
实现代码
1 |
时间复杂度O()
空间复杂度O()
利用贪心算法解决背包问题的关键是如何选定贪心策略,使得物品按照这个策略能够尽可能的装入背包中,最后价值最大。很明显,我们既不能仅着眼于看见价值最大的物品即装入而忽略重量的盲目追求价值的策略,因为这样背包可能会迅速装满;也不能仅着眼于每次选择最轻的物品来使得背包能装更多的物品,这个策略最后的结果价值不一定是最大。而正确的,应该根据性价比来选择物品。
因此,我们的算法可以设计为:
- 根据给定的物品重量和价值,计算每一个物品的单价;
- 再根据得到的单价对每一个物品进行降序排列;
- 根据得到的物品优先级次序来装入背包,这里区分是一般的背包问题还是0-1背包问题。若是前者,可以根据背包剩余的容量来计算装入物品的多少
( 0<实际装入的w[i]<1 ),直到背包装满,可以得到最优解。若是后者,则根据背包的容量是否够继续装入下一个物品,够则装入,不够则跳过当前物品去判断下一个物品,直到背包装满或没有适合的物品装入为止,只能尽可能的靠近最优解。
顺便实现一下?😏😏——代码在题目收缩面板里呢!!!
3.最小生成树——Prim为例
最小生成树问题最常见的算法是Prim算法和Kruskal算法,它们都可以在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之和亦为最小。
先来简单认识一下这两个算法:
Prim算法
Prim算法的基本思想是通过将已访问节点和未访问节点分开,每次从所有已访问节点中的任一节点出发,逐步通过可达边中的最短边将未访问节点纳入已访问节点的阵营中,直到未访问节点阵营全部进入已访问阵营中,得到最小生成树。
具体算法看WIKI:
Kruskal算法
Kruskal算法的基本思想是通过将点边分离再组合得到最小生成树,即将所有的边按从小到大排序,每次任意选取最小的一条边,如果这条边连接的两个点至少有一个不在正在建立的连通图中,那么将这条边添加到图中。不断重复,直到所有的点都连接在一起且不构成圈,或者说同在一个连通分量。
具体算法看WIKI:
- 新建图G,G中拥有原图中相同的节点,但没有边;
- 将原图中所有的边按权值从小到大排序;
- 从权值最小的边开始,如果这条边连接的两个节点于图G中不在同一个连通分量中,则添加这条边到图G中;
- 重复3,直至图G中所有的节点都在同一个连通分量中。
顺便实现一下?😏😏——这里实现Prim算法
Prim
如下图,从A节点开始,求它的最小生成树。
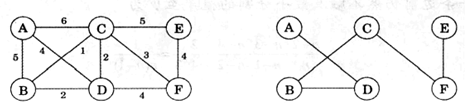
基本思路:思路还是Prim算法的思路,实现是利用两个数组来表示已访问节点(selected[])和未访问节点 (left[]),利用二维数组graph[][]的邻接矩阵来存储图。每一次找点,都是从所有已访问节点数组(selected[])出发任选一个点,找到最短的可达边,且对应的点在未访问节点数组(left[])中,避免重复也要求不在已访问节点数组(selected[])中。每次找到都将点从未访问搬到已访问中。
1 |
|
注:看到别的dalao以及wiki上写的真的是头大,这是自己基于Prim思想写的,在二维数组中各种花里胡哨的操作。时间复杂度嘛,不敢说,only achieved!!!另外,代码还是具有可复用性的嘛。👀🌚
4.多级调度问题
有n个作业,完成作业的耗时分别为T1,T2,T3,...,Tn,一共有m台机器(m<n),每个作业为非抢占式,问如何安排作业才能使得完成所有的作业耗时最少?看个例子:
作业调度
例如n=7,m=3,每个作业完成所需的时间如表所示
| 作业编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 完成用时 | 2 | 14 | 4 | 16 | 6 | 5 | 3 |
算法可设计为:
- 将所有的作业按所用时间大小从大到小排序;
- 根据作业次序,按
M1 ~ Mm的工作量从小到大分配,工作量即已安排的作业的时间叠加,谁的工作量小就把一个作业分配给谁。 - 不断重复步骤2,直到分配完毕。最后工作量最大的机器的工作量就是完成所有作业的最短时间。
- 机器与机器之间是并行关系。
贪心算法的应用还有很多,比如哈夫曼编码和旅行商问题等。应用不可能面面俱到,最核心的还是要掌握算法的思想,利用思想去举一反三,解决变化多样的问题。
三、总结一下
最后稍微总结一下贪心算法,先再看一波概念,希望有所体会或新的收获。
贪心算法就是在一个大问题中,朝着总目标的最终解前进,每到一个状态选择当前的最优解,不断重复。最后将得到的所有解组合为最终的一个可行解。它适用前提是:局部最优策略能够导致产生全局最优解。否则,不适用。
最后,贪心算法并不是解决最优化问题的最好方法,它只是其中一个可行方法,它得到的解不一定是最优的,且大多数问题都不是最优的。但使用这个算法得到的解可以作为取得最优解的参考。
balabala~~,实现算法太难了😫😫
参考
- 维基百科
- 《算法设计与分析》——吕国英
- 【算法】—-贪心算法(背包问题)





